01 两数之和,三数之和
1、两数之和
-
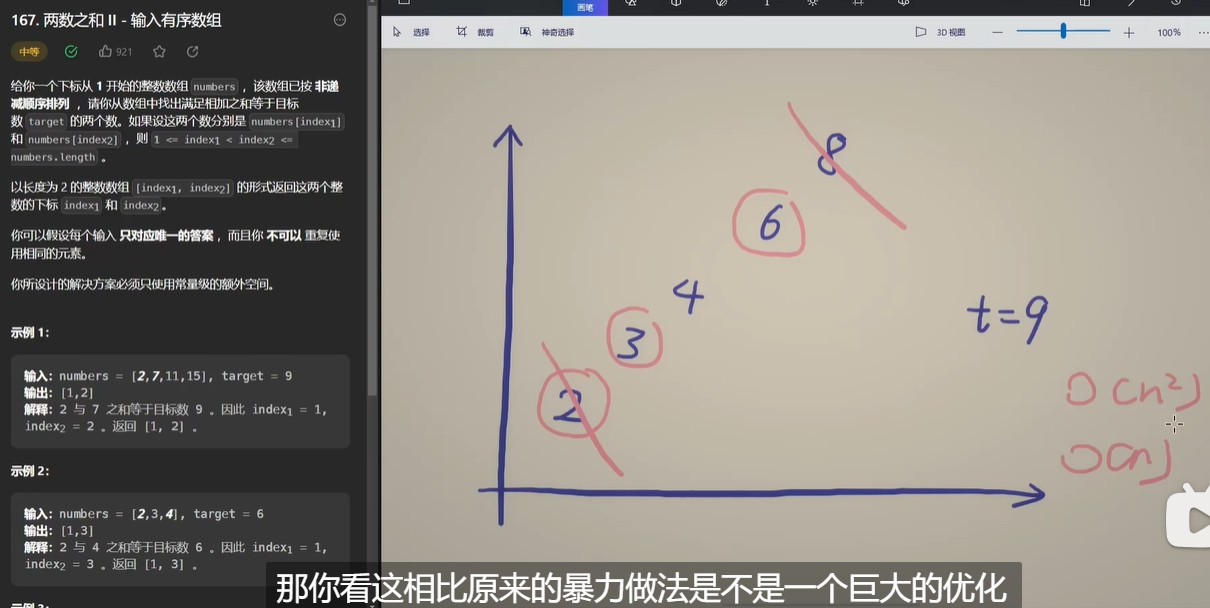
问题描述:在有序数组中找俩数(唯一)使得两数之和等于target
-
问题思考:如果用暴力的话,时间复杂度为O(n²),现在我们要求用O(n)的方法去做,那么就想到利用原序列有序的这个条件(如果暴力就没用到,我随便一个序列也可以)
-
(其实无序的话你开始排个序就好了)
利用有序,我们就可以发现可以去掉一些一定不符合的数字。比如最小的2+8>9了,说明8跟谁都不能合成target9,所以去掉8,右指针向左移动。这时候我们再看第二大的6,第二大的6+2<9,说明2跟谁都不能合成target了,所以去掉2,左指针向右移动。
所以我们可以发现,这样就有一种双指针的方法,把最后的答案区间锁定在左右指针之间。(当前最小的数和当前最大的数加起来跟目标比一比)注意:只有有序的数组才能使用这个算法。
- 算法核心:
-
while(left < right)
-
如果左右指针的数合起来刚好等于target,那就返回结果
-
如果...大于target,那么右指针向左移动一格
-
如果...小于target,那么左值真向左移动一格
2、三数之和(变异版两数之和)
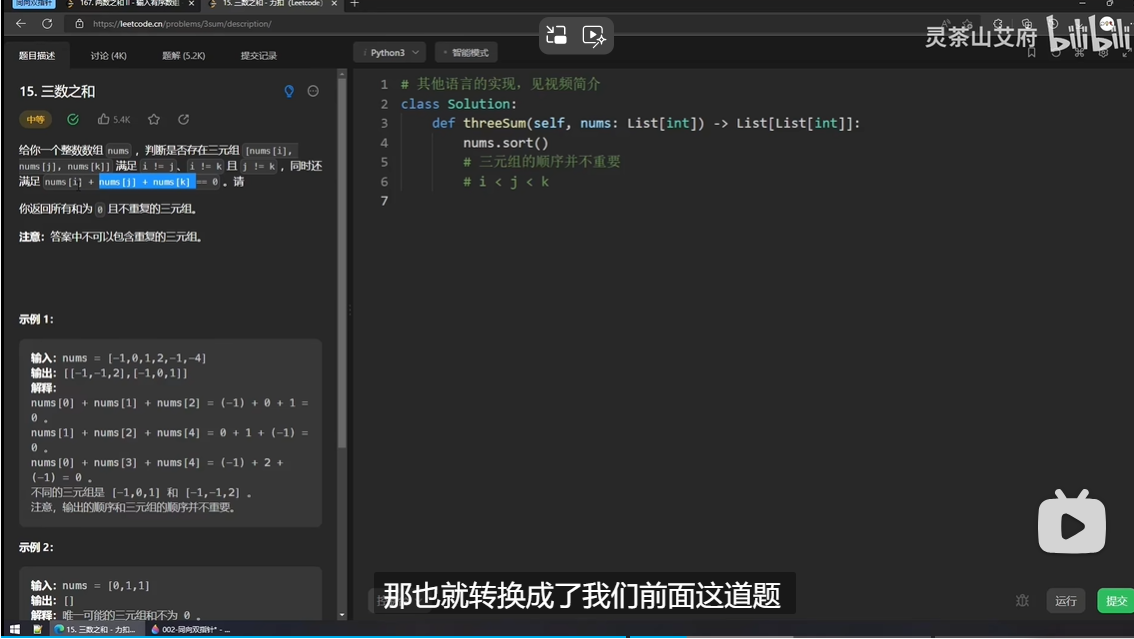
这个也要有序!所以一开始上来就给这个数组排序。
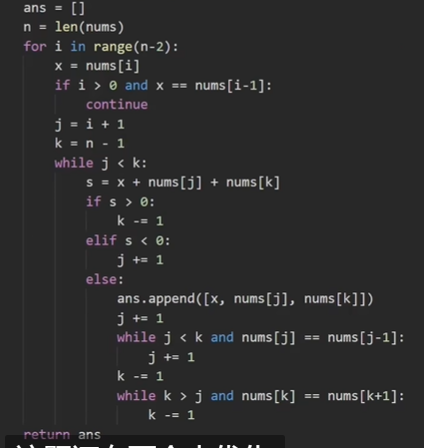
这题其实也可以转化成两数之和,我们枚举nums[i],然后让newTarget = target - nums[i] ,这样就变成了前面的n次的两数之和。
然后题目要求要去除同样的三元组(比如如果有两个-1都满足,那么-1可能会出现两次)这种情况下不能去重(因为可能两个-1都要用到),那么怎么办呢?既然说三元组和组内的顺序不重要,那么我们就人为规定一个顺序(i<j<k)。然后如果下一个数字和当前这个数字是相同的,那么就跳过。
02 承最多水的容器 接雨水
1、承接最多水的容器
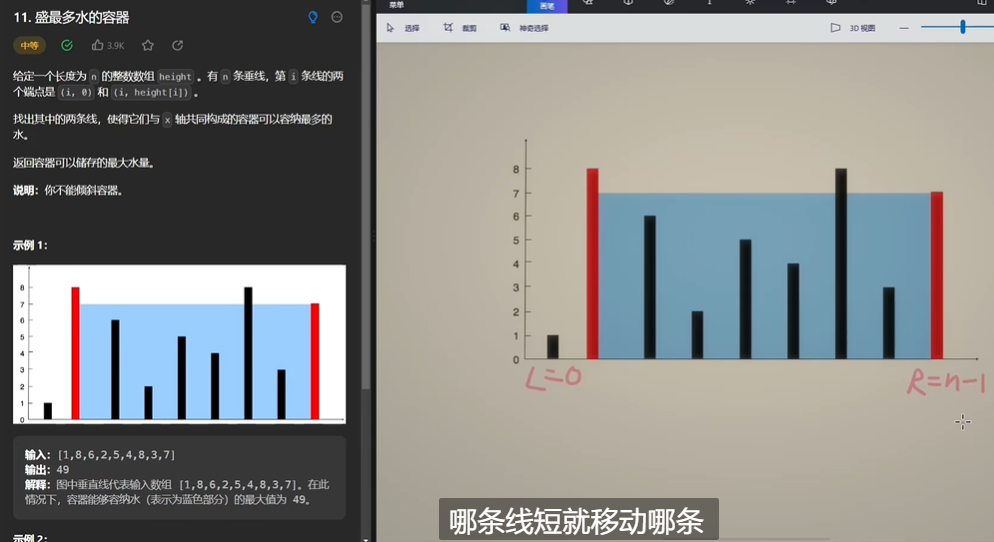
- 问题描述:这就不描述了,看图就能理解。额外的提示是这题如果用n²会超时,所以肯定不能模拟啦
- 问题思考:其实这题的想法还是双指针,左右指针向中间移动,哪条短就移动谁(不能让人家长的又变短宽度又变窄吧,那一定更小了),然后每次移动更新最大值。一样长就移动哪个都可以。
- 每次花费O(1)的时间就去掉了一根线,所以总的时间复杂度是O(n)
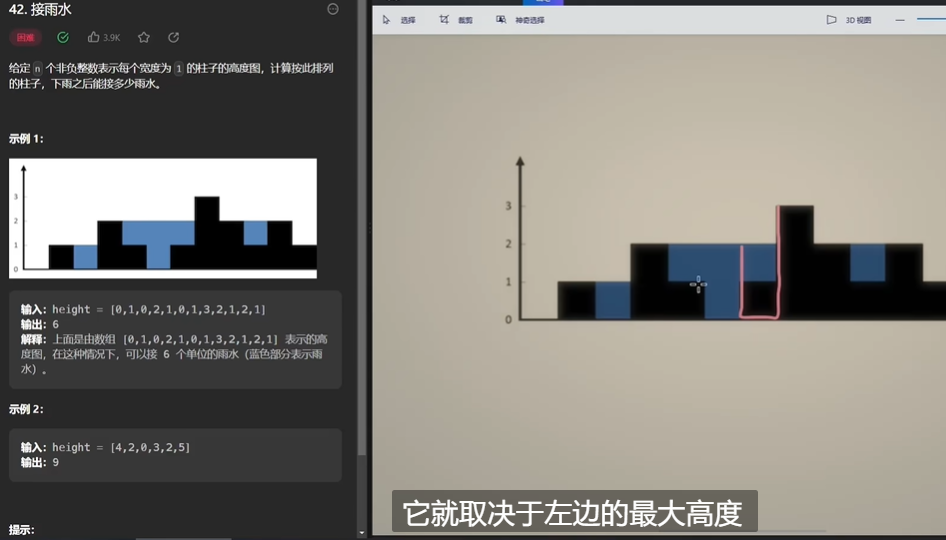
2、接雨水
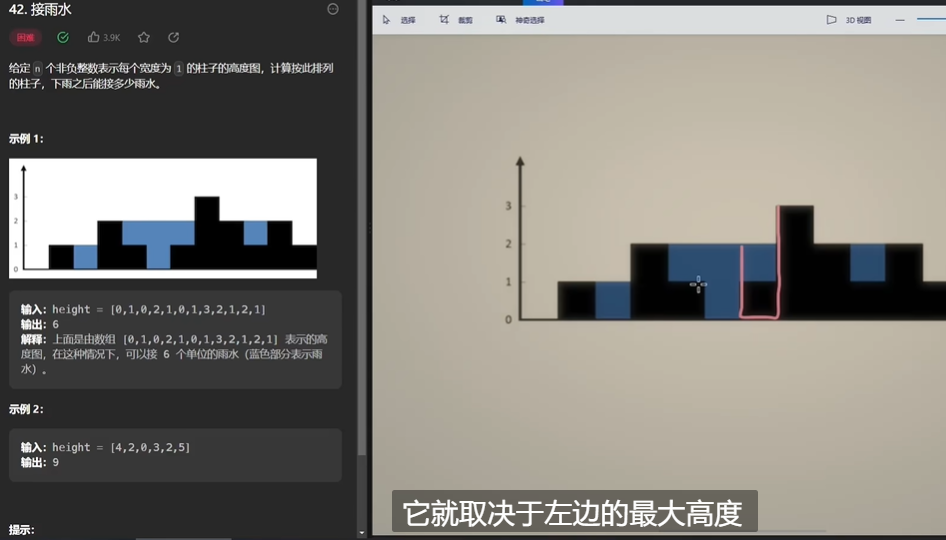
问题描述:这个也没啥好说的
问题思考:按单位来算,这个格子所能承的水,左边取决于左边的最大高度,右边取决于右边的最大高度,两个高度取最小值,然后减去这个位置的格子高度,就是这个位置所承接的水的数量
算法:开两个额外数组,一个存最左边到i的最大高度(前缀最大值),一个存i到最右边的最大高度(后缀最大值)
时间复杂度:都是一次遍历,所以O(n)
优化:如果前缀最大值比后缀最大值小,那么这个位置能装的量就是前缀最大值,并且向右扩展;如果后缀最大值比前缀最大值小,那么这个位置能装的量就是后缀最大值,并且向左扩展(没太看懂)