Daonan's Blog

01 两数之和，三数之和

1、两数之和

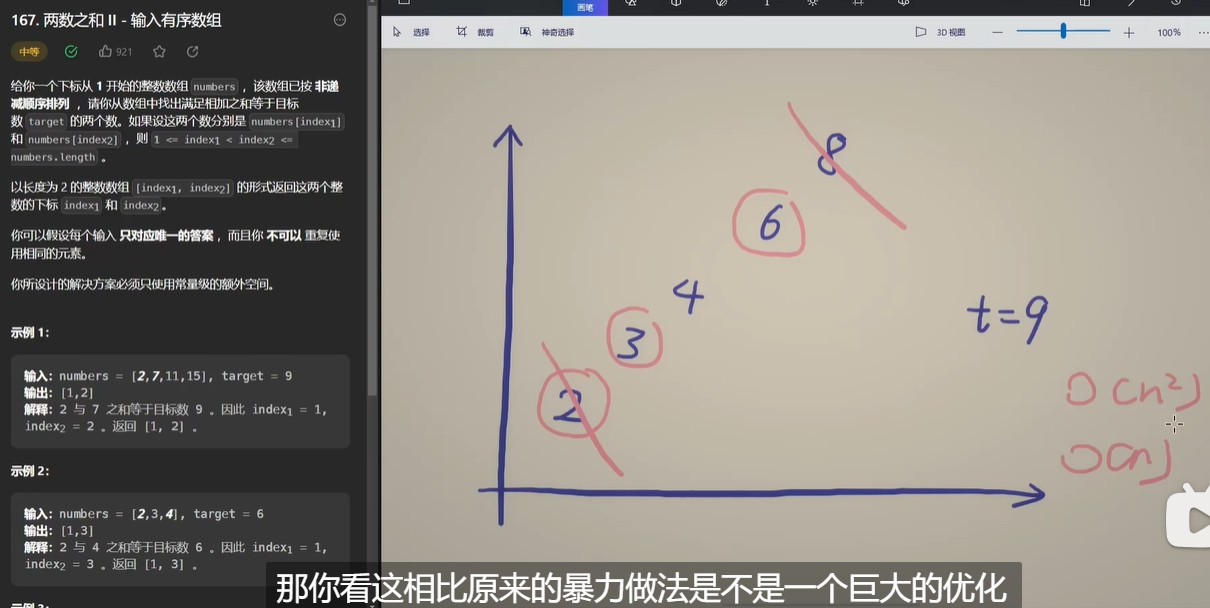
问题描述：在有序数组中找俩数（唯一）使得两数之和等于target
问题思考：如果用暴力的话，时间复杂度为O(n²），现在我们要求用O(n)的方法去做，那么就想到利用原序列有序的这个条件（如果暴力就没用到，我随便一个序列也可以）
（其实无序的话你开始排个序就好了）

利用有序，我们就可以发现可以去掉一些一定不符合的数字。比如最小的2+8>9了，说明8跟谁都不能合成target9，所以去掉8，右指针向左移动。这时候我们再看第二大的6，第二大的6+2<9，说明2跟谁都不能合成target了，所以去掉2，左指针向右移动。

所以我们可以发现，这样就有一种双指针的方法，把最后的答案区间锁定在左右指针之间。（当前最小的数和当前最大的数加起来跟目标比一比）注意：只有有序的数组才能使用这个算法。

算法核心：

while（left < right)
如果左右指针的数合起来刚好等于target，那就返回结果
如果...大于target，那么右指针向左移动一格
如果...小于target，那么左值真向左移动一格

2、三数之和（变异版两数之和）

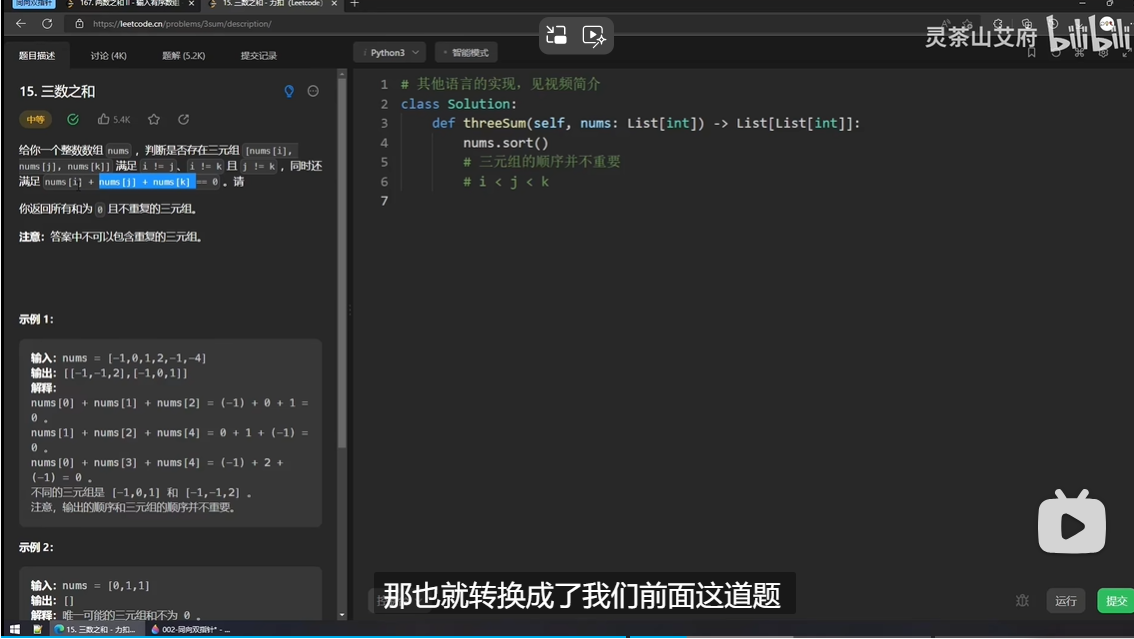
这个也要有序！所以一开始上来就给这个数组排序。

这题其实也可以转化成两数之和，我们枚举nums[i]，然后让newTarget = target - nums[i] ，这样就变成了前面的n次的两数之和。

然后题目要求要去除同样的三元组（比如如果有两个-1都满足，那么-1可能会出现两次）这种情况下不能去重（因为可能两个-1都要用到），那么怎么办呢？既然说三元组和组内的顺序不重要，那么我们就人为规定一个顺序（i<j<k)。然后如果下一个数字和当前这个数字是相同的，那么就跳过。

02 承最多水的容器接雨水

11、承接最多水的容器

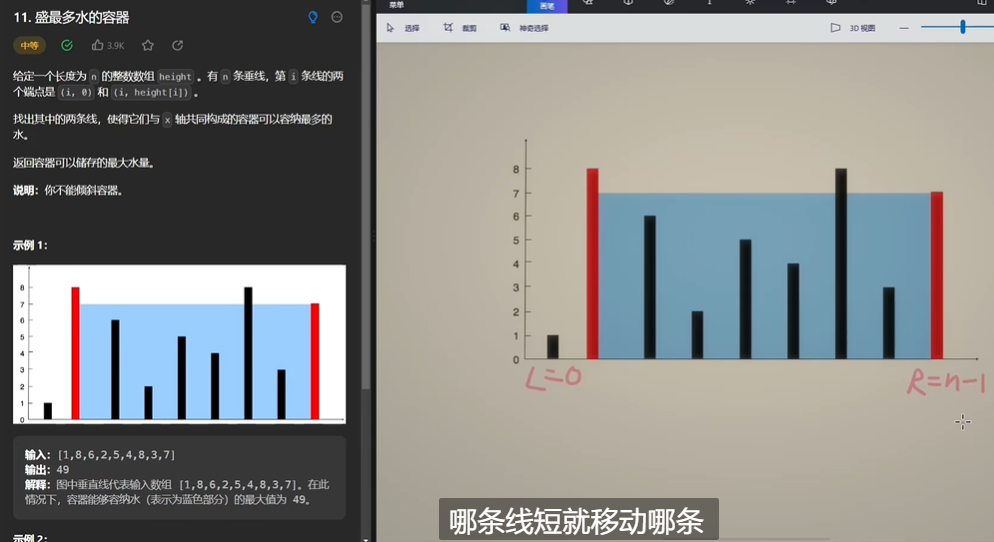
问题描述：这就不描述了，看图就能理解。额外的提示是这题如果用n²会超时，所以肯定不能模拟啦
问题思考：其实这题的想法还是双指针，左右指针向中间移动，哪条短就移动谁（不能让人家长的又变短宽度又变窄吧，那一定更小了），然后每次移动更新最大值。一样长就移动哪个都可以。
每次花费O(1)的时间就去掉了一根线，所以总的时间复杂度是O(n)

42、接雨水

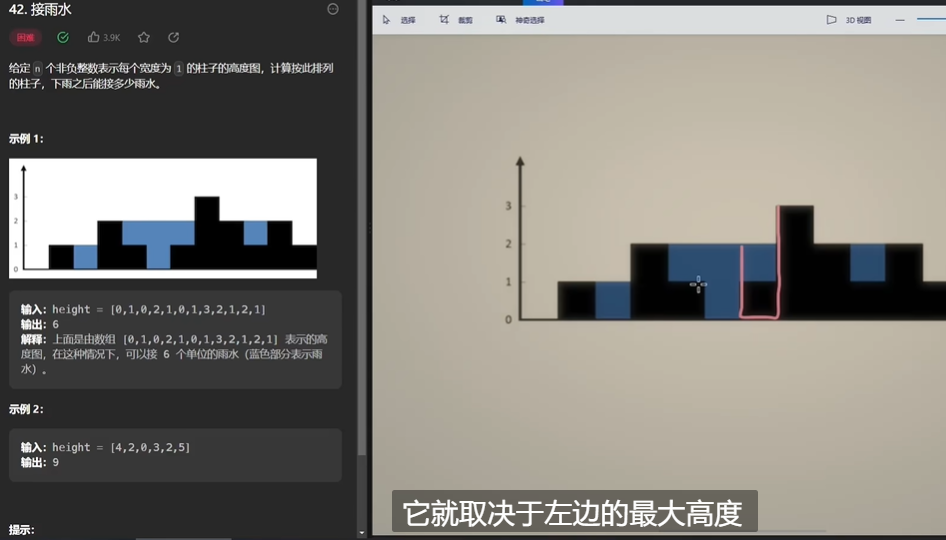
问题描述：这个也没啥好说的

问题思考：按单位来算，这个格子所能承的水，左边取决于左边的最大高度，右边取决于右边的最大高度，两个高度取最小值，然后减去这个位置的格子高度，就是这个位置所承接的水的数量

算法：开两个额外数组，一个存最左边到i的最大高度（前缀最大值），一个存i到最右边的最大高度（后缀最大值）

时间复杂度：都是一次遍历，所以O(n)

优化：如果前缀最大值比后缀最大值小，那么这个位置能装的量就是前缀最大值，并且向右扩展；如果后缀最大值比前缀最大值小，那么这个位置能装的量就是后缀最大值，并且向左扩展（没太看懂）

03 滑动窗口问题

209、长度最小的子数组

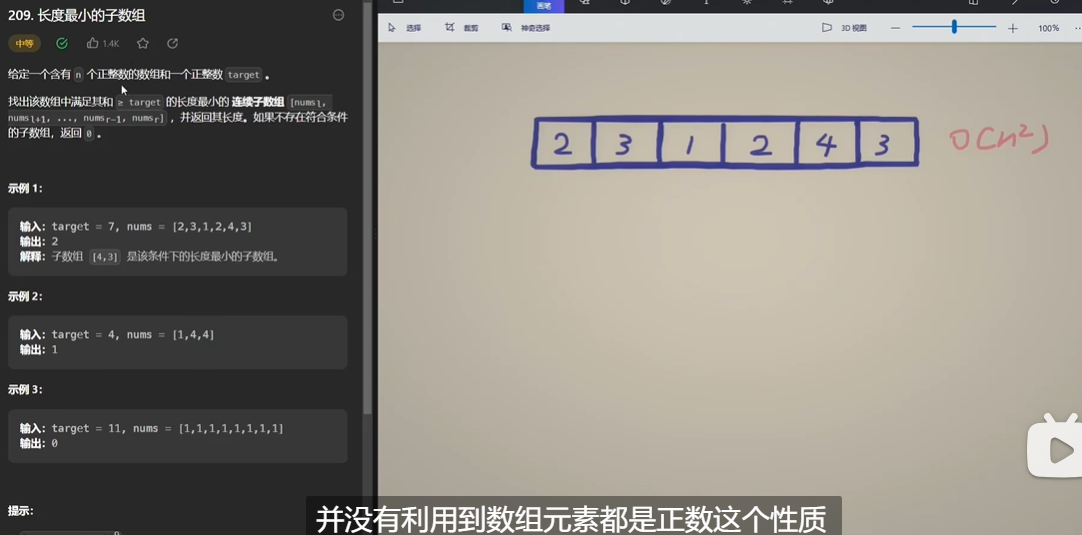
问题描述：一个正整数序列（非有序）和一个正整数target，在正整数序列中找出满足和≥target的连续子数组，并返回长度，没有返回0。
问题思考：利用数组里面都是正整数的性质，保留上一次计算的结果，比如如果四个数大于target，那么五个数也会大于target。所以我们得到一串大于等于target的时候，这时候我们让左端点向右移动来缩小，看缩小后还是不是大于target。所以我们就得到了一个方法：枚举右端点，缩小左端点，然后就能找到最小的数组了。
时间复杂度：O(n)（为什么两层循环还是o(n)呢？因为其实左指针总共就动了n次，没有每次右指针向前他就从头开始，而是从当前位置继续）

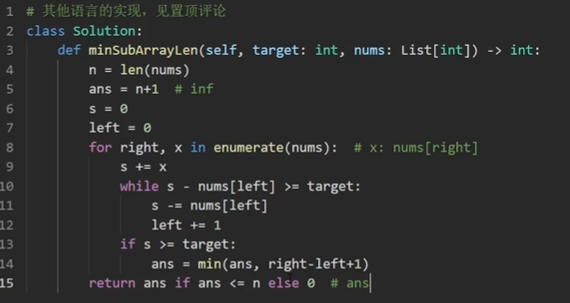
具体解释：还是设左右指针，for循环遍历右指针，然后要把当前遍历到的值新加到总和s里面去，left是不用更新的，然后开始向左移动，移动到刚好大于等于target就停止。（这边为什么14行要加1？自己假设一下left和right指向同一个，那么这时候长度是1）然后更新最小长度。最后判定一下最小长度如果大于n，那么就说明全部加起来都不到target，返回0.

04 二分查找红蓝染色法

34、在排序数组中查找元素的第一个和最后一个位置

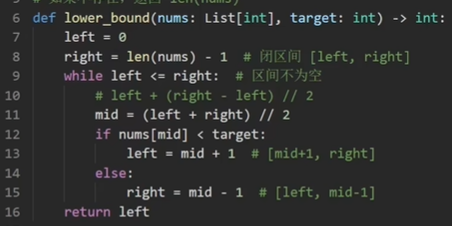
这边有个小例子，注意这里的左右边界（L、M）都是闭区间！所以更新的时候，L=M+1，R=M-1。不这么弄最后L=M没找到的时候和找到的时候都是一样的，会进入死循环。

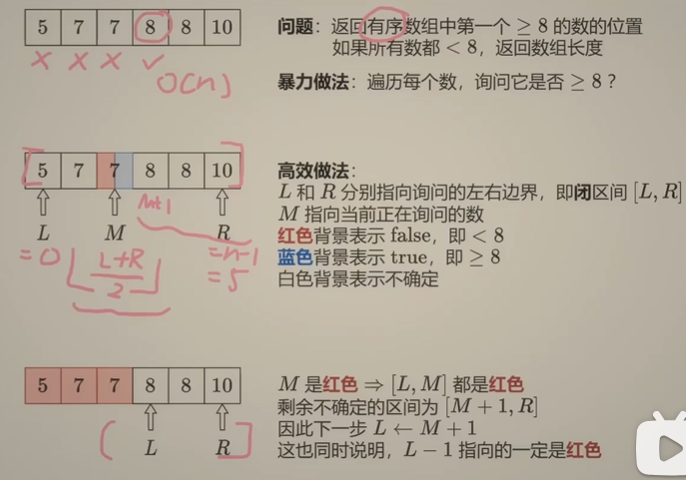
L-1指向的一定是红色，R+1指向的一定是蓝色

如果没找到的话，L是会一直向右移动的，最后L等于数组长度（不用-1！）

ps：这边（left+right)/2 在java和c++可能会有溢出的问题，改写成 left + ( right - left ) / 2，这其实就是个二分的问题。

有＞、≥、＜、≤等多种考法，但是其实方法上是一样的：

＞x等价于 ≥ x+1（对于整数来说）
< x等价于 ≥ x的那个数的左边
≤ x等价于＞x的那个数的左边

最后，让我们来看这道题：

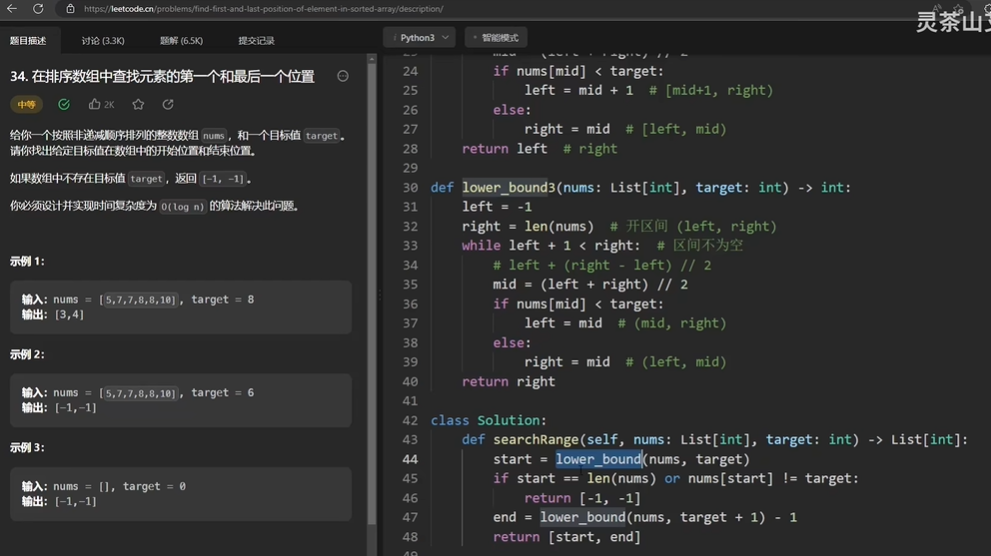
问题描述：给一个非递减整数数组，在数组里面找目标值的开始位置和结束位置，也就是找小于等于他和大于等于他位置。
问题思路：已经全写上面了。

05 二分查找数组峰值搜索旋转排序数组

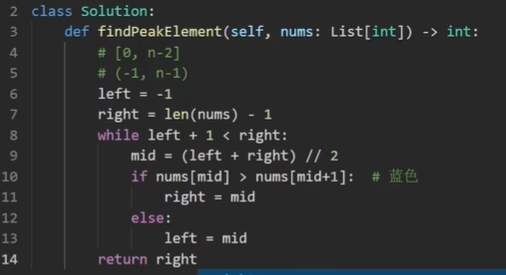
162、寻找峰值

问题描述：在一个整数数组里面找到一个数字比其左右相邻的数都大，这个数字就称为峰值元素。用o(logn)的时间找到任何一个峰值元素所在位置就行。
问题思路：一样用二分的方法，说实话我没咋看懂啊，写当然我会写

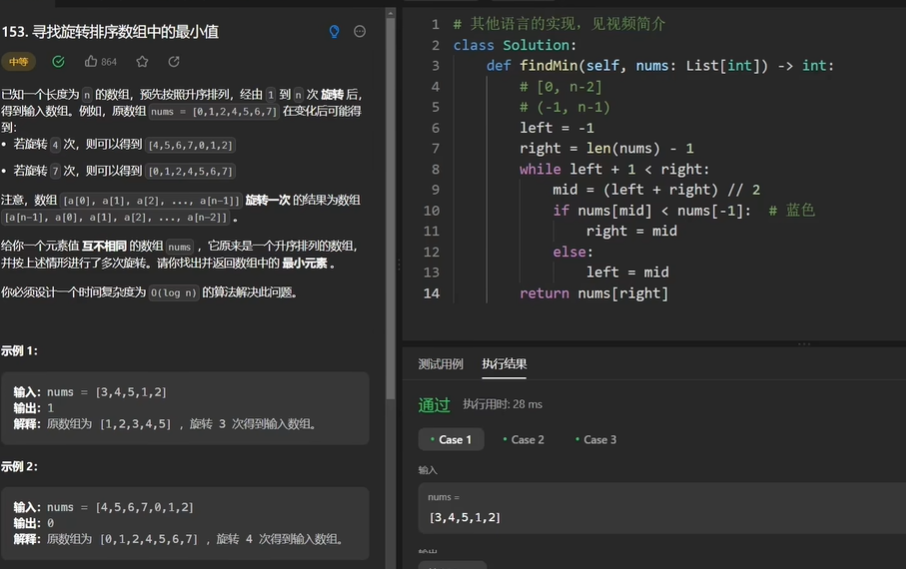
153、寻找旋转排序数组中的最小值

06 反转链表

206、反转链表

要修改一个指针的指向，只用一个指针cur表示当前遍历到的节点是不够的，因为重新指完方向后，cur原本的next就找不到了。所以我们还需要一个nxt指针在重新指方向之前保存cur原来的next是谁。

然后做法就是把cur更新成nxt，nxt更新成cur->next（新的cur）

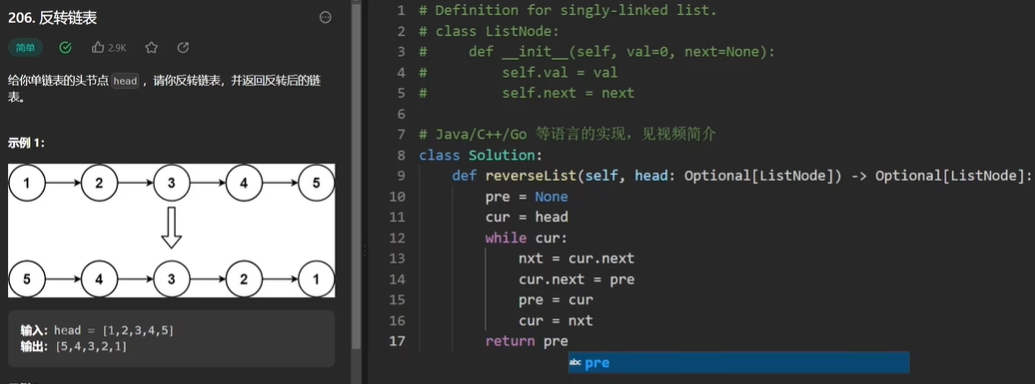
时间复杂度：O(n)
空间复杂度：O(1)

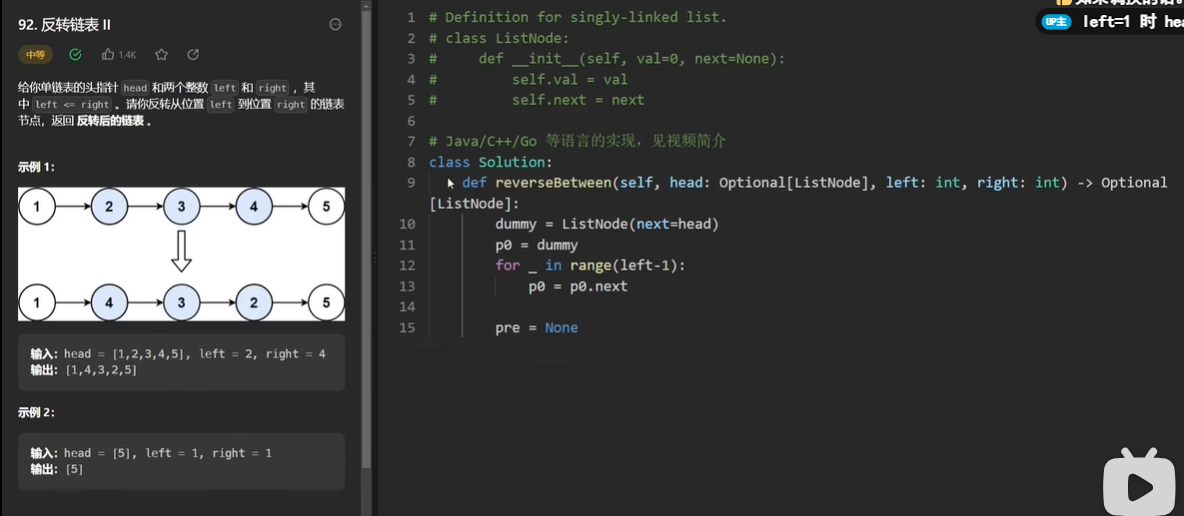
92、反转链表II

除了整个链表反转的，也有部分链表反转的。这种问题在遇到一些特殊情况的时候，是要记得看第一个头节点要不要进行反转的。如果需要头节点一起反转的话，就设置一个dummyNode（哨兵节点）。

07 动态规划入门

198、打家劫舍

问题描述：小偷偷房子里的钱，两间相邻的房子都被偷了的情况下小偷就会被抓。已知每个房子的钱的数量数组，求小偷偷的钱最多能多少。
问题思路：把一个大问题变成规模更小的子问题。从第一个房子或者最后一个房子开始思考（因为收到的约束最小），现在我们从最后一个房子开始考虑选或者不选。
1. 如果选，那么问题就变成n-1个房子的问题
2. 如果不选，那么问题就变成n-2个房子的问题（因为n-1就选不了了）

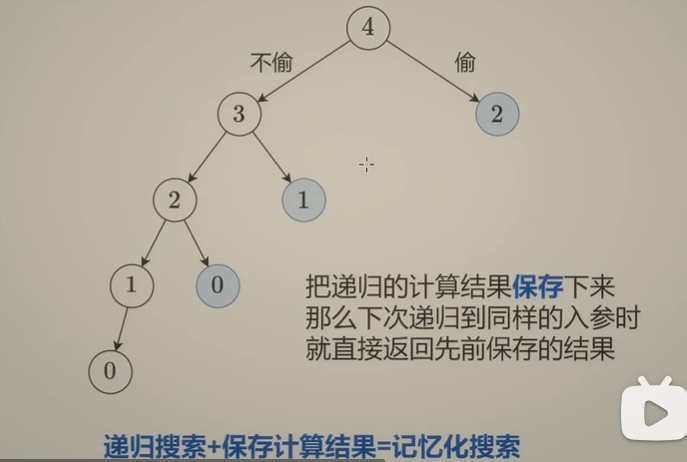
所以我们就可以抽象出来一个搜索树

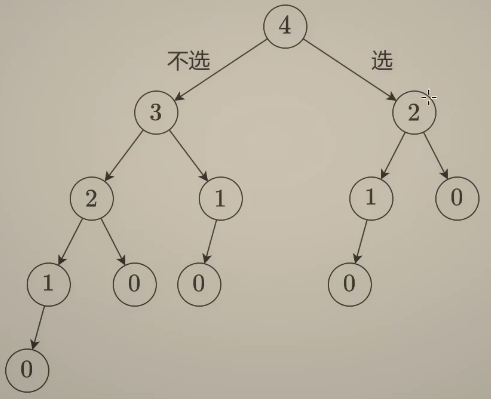
然后我们再抽象一下，写出递归公式

dfs(i-1)就是第i个房子不选的情况，dfs(i-2)+nums[i]就是第i个房子选的情况。

但是我们如果就这么简单写回溯代码的话，因为递归的时间是O(nlogn)，这么写会超时，所以我们需要进行简化（剪枝）。比如我们这边2-1-0-0的dfs(2)算了两遍，所以我们可以进行简化。

怎么剪枝呢，我们可以创建一个memo数组或者哈希表。这样当我们计算到重复的值的时候，就可以直接返回memo里面保存的结果了。这样我们就成功把时间复杂度降低到了O(n)

class Solution {
    private int[] nums, memo;
    public int rob(int[] nums) {
        this.nums = nums;
        int n = nums.length;
        memo = new int[n];
        Arrays.fill(memo, -1); // -1 表示没有计算过
        return dfs(n - 1); // 从最后一个房子开始思考
    }
    // dfs(i) 表示从 nums[0] 到 nums[i] 最多能偷多少
    private int dfs(int i) {
        if (i < 0) { // 递归边界（没有房子）
            return 0;
        }
        if (memo[i] != -1) { // 之前计算过
            return memo[i];
        }
        int res = Math.max(dfs(i - 1), dfs(i - 2) + nums[i]);
        memo[i] = res; // 记忆化：保存计算结果
        return res;
    }
}

这边时间复杂度怎么算呢，就是用状态个数乘上单个状态所需要的计算时间。