串
1.定义:
即字符串(String),是由零个或多个字符组成的有限序列,一般记为S=‘a1a2a3…an' (n>=0)
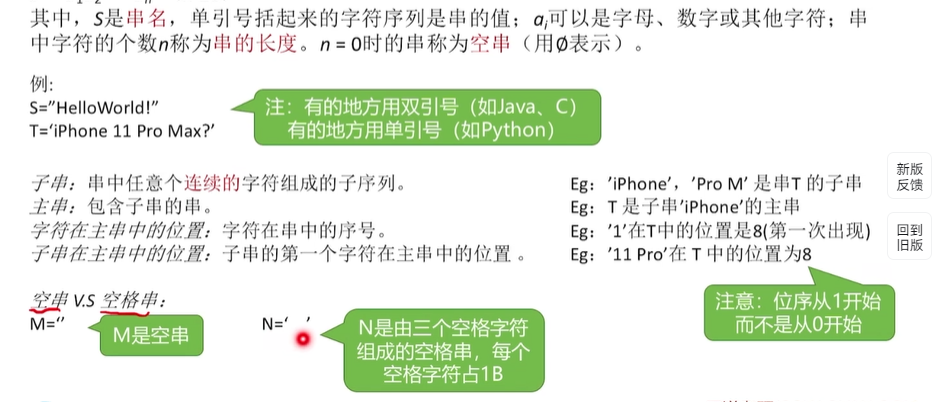
1.(位序从1开始而不是0!)
2.空串:长度为0(即不含任何字符)的串
3.空格串:由空格组成的非空串
2.串的基本操作:

常考的:
Concat(&T,S1,S2)
SubString(&Sub,S,pos,len),pos为1开始
StrCompare(S,T)
Index(S,T)
总结:

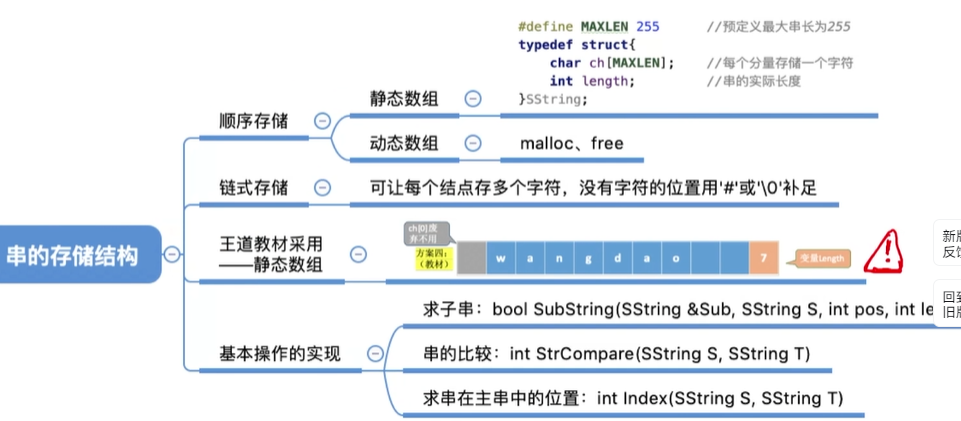
## 串的存储结构 **1.顺序存储结构定义:**
1.静态数组(不可变的)

2.动态数组(堆分配存储)

注意:ch[0]存储数组长度
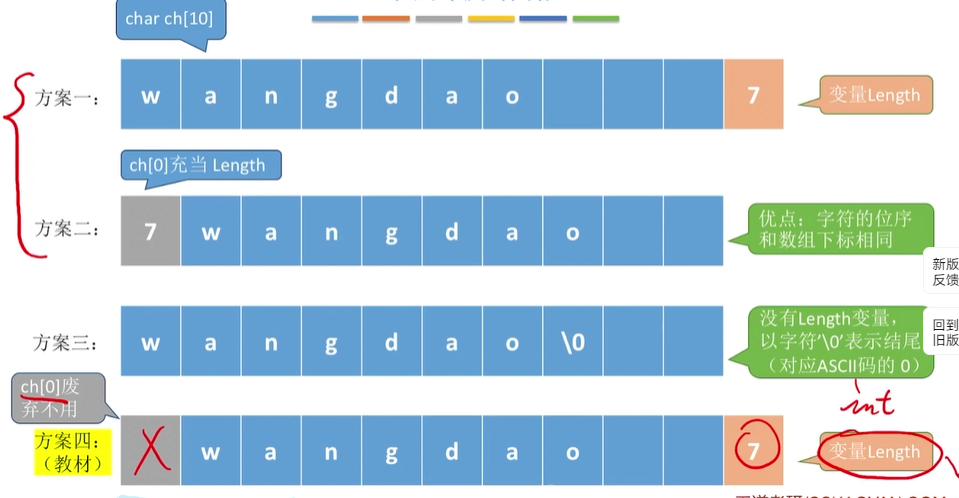
教材使用的是,首位置废弃不用,但是同样记yigelength(若放在ch[0]只能存储到255
2.链式存储结构定义:
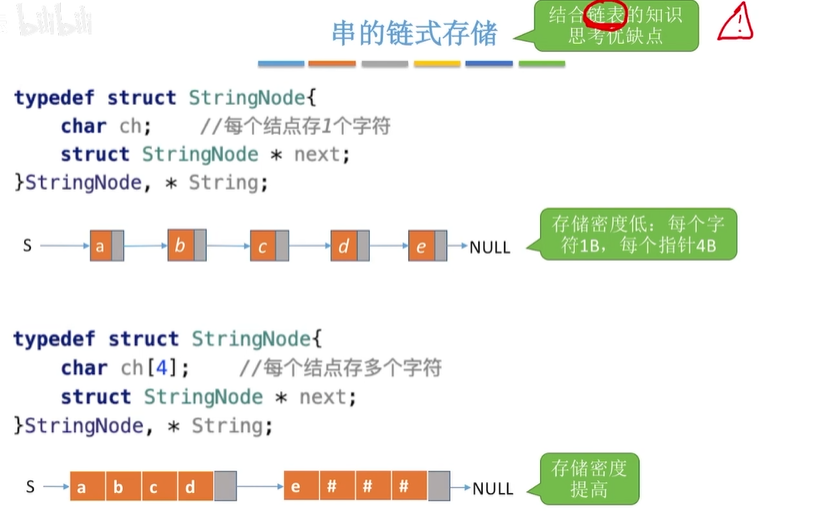
3.串的一些基本操作的实现:(基于顺序定长存储)
1.返回某位置后面的定长子串SubString(&Sub,S,pos,len) ,用Sub返回
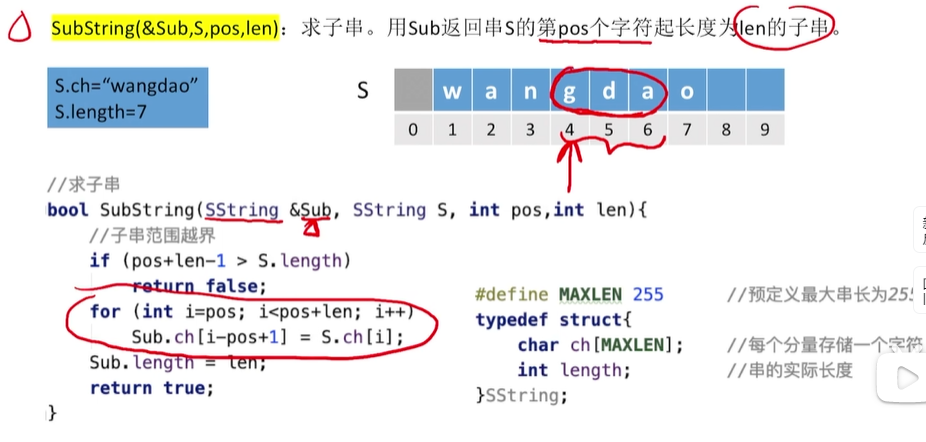
2.比较操作(S,T)

3.定位操作Index(S,T)

总结:
## 串的模式匹配 **1.定义:** 再主串找到与模式串相同的子串,并返回他的位置
朴素的模式匹配算法:狠狠的暴力!
若模式串的长度为m,主串长度为n,则
1.
匹配成功的最好时间复杂度为O(m)
匹配失败的最好时间复杂度:O(n-m+1) =O(n-m)≈O(n)

## KMP算法 **1.算法进入**  从主串第一个开始,如果l后面不是e,那么也不用回溯了,因为我们知道主串第二个也不会符合模式串第一个。后面几个也同理 所以 我们就直接从l后面开始! ——>如果j=k的时候才发现匹配失败,说明1~k-1都匹配成功
意思就是 :如果到最后一个才发现错了
对于主串,就算不匹配了,指针也不回溯!
对于子串,指针则要返回到串首,狠狠的回溯!
算法实现:
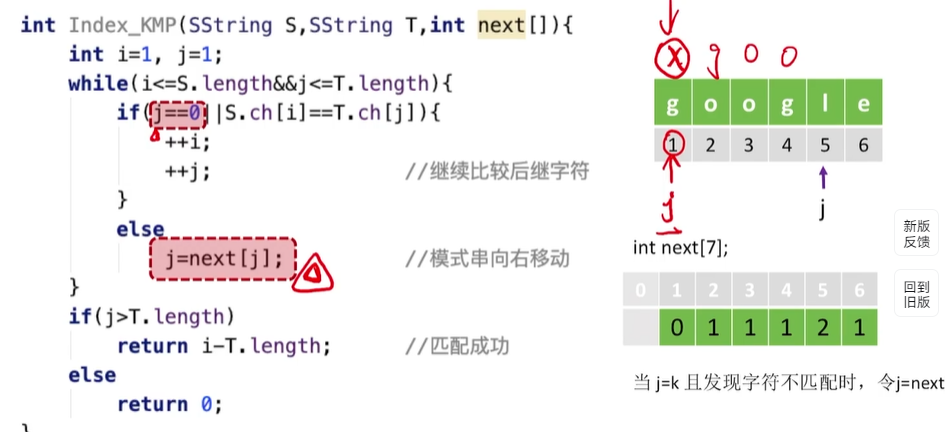
重点来力!如何构造next数组!
两个例子:
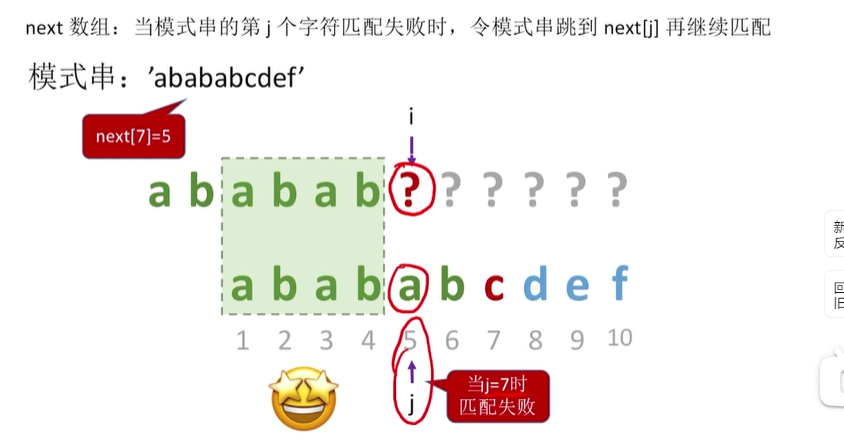


练习:
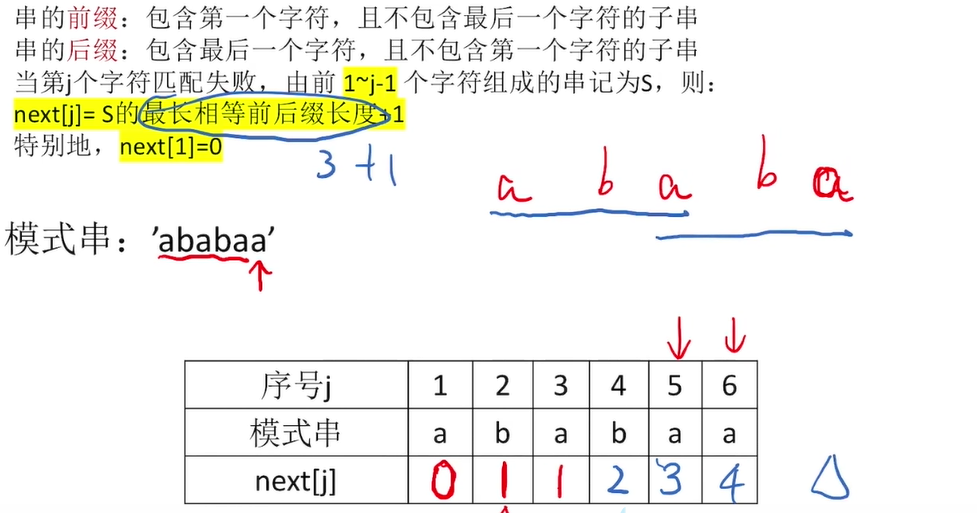
这里,特别的,next[1]=0,next[2]=1;
然后就是对比前缀的子串和后缀的子串最多能相同的个数
比如上面的第六个,它前面的为ababa,
那么前缀就是abab及其子串,后缀就是baba及其子串
那么当前缀的字串为aba,后缀字串为aba的时候, 一样的最多为3个
所以,3+1=4
最终,我们的求next数组和KMP算法是这样的!
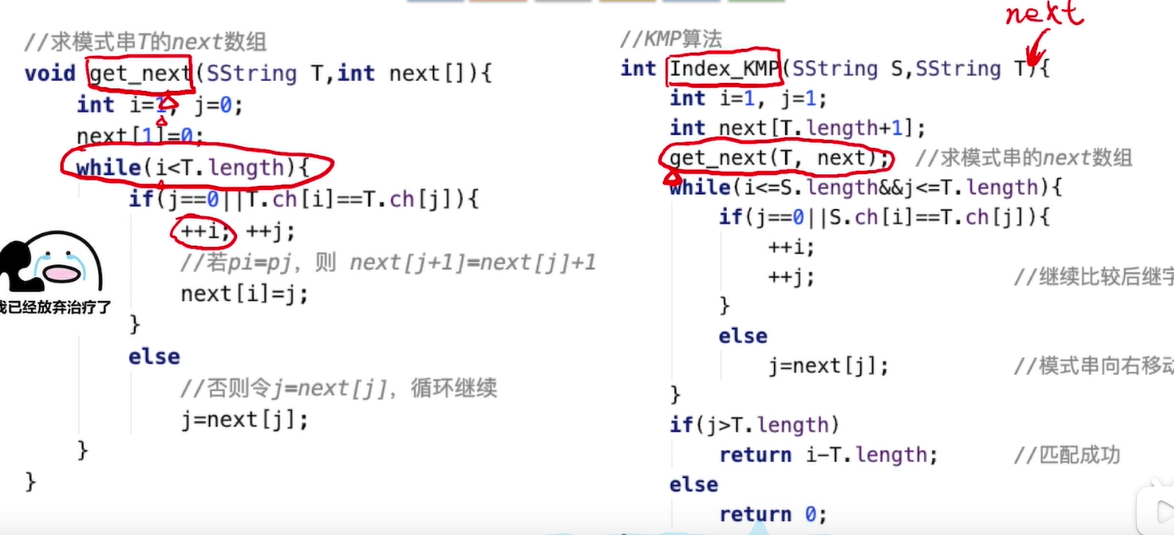
总结:

还有一种 优化的KMP算法(把next数组优化成nextval数组,减少了几次无用的判断)
